생존 분석은 관심 이벤트까지의 예상 시간을 조사하기 위해 널리 사용되는 통계 방법입니다.
| 의약품 |
|
| 프로젝트 |
|
| 경제 |
|
| 인적자원부 |
|
어치버스의 직원 참여 및 유지 보고서에 따르면 직원의 52%가 2021년에 새 직장을 찾을 계획이며, 최근 31개국 30,000명 이상의 직원을 대상으로 한 설문조사에 따르면 40%가 직장을 그만둘 것을 고려하고 있는 것으로 나타났습니다. Forbes는 주로 팬데믹 고갈, 대규모 인재 이주를 예측하는 Linkedin 전문가, #Great Resignment 및 #Great Reshuffle 주제로 인해 이러한 추세를 “Turnover Tunami”라고 부릅니다. 논의하다.
언제나처럼 데이터직원 참여 및 유지에 대한 통찰력을 얻으면 이직률을 줄이고 참여도가 높고 참여도가 높으며 만족도가 높은 팀을 구축하는 데 도움이 됩니다.
다음은 HR 팀이 직원 이직률 데이터에서 발견할 수 있는 몇 가지 예입니다.
- 남아있거나 떠나는 직원들의 구체적인 특징은 무엇입니까?
- 직원 그룹마다 이직률이 비슷합니까?
- 직원이 일정 시간이 지나면 퇴사할 가능성은 얼마나 됩니까? (즉, 2년 후)
데이터 선택
캐글 제공 IBM에서 생성한 가상의 직원 이직률 및 성과 데이터 세트직원 이직률 및 중요한 직원 특성을 조사하여 기존 직원의 생존 시간을 예측하는 데 사용됩니다.
생존 기능 개념
이벤트삶/죽음 또는 체류/휴가와 같은 흥미로운 경험
생존 시간관심 이벤트 전 시간입니다.그 데이터에서 직원이 퇴사하기 전까지의 기간
질문 검토
검열된 관찰(검열 관측)누군가에 대한 이벤트가 기록되지 않은 경우 이벤트 시간 데이터에 나타납니다.이는 크게 두 가지 이유 때문일 수 있습니다.
- 이벤트가 아직 발생하지 않은 경우(예: 생존 시간을 알 수 없음/사임하지 않은 사람에게 오해의 소지가 있는 경우)
- 데이터 손실(즉, 손실) 또는 연락 지점 손실
검토 질문 유형
- 왼쪽 관찰자(왼쪽 검열됨): 생존기간이 관찰기간보다 짧다
- 오른쪽(오른쪽 검열): 생존기간이 관찰기간보다 길다
- 간격 – 잘림(간격 중도절단됨): 수명을 정확하게 정의할 수 없음
가장 일반적인 유형은 우측 관측 중단(오른쪽 검열)일반적으로 생존 분석을 통해 처리됩니다.
그러나 다른 두 개는 추가 조사가 필요할 수 있는 데이터의 문제를 나타냅니다.
아래 다이어그램과 같이 유형이 구성되는 방식입니다.
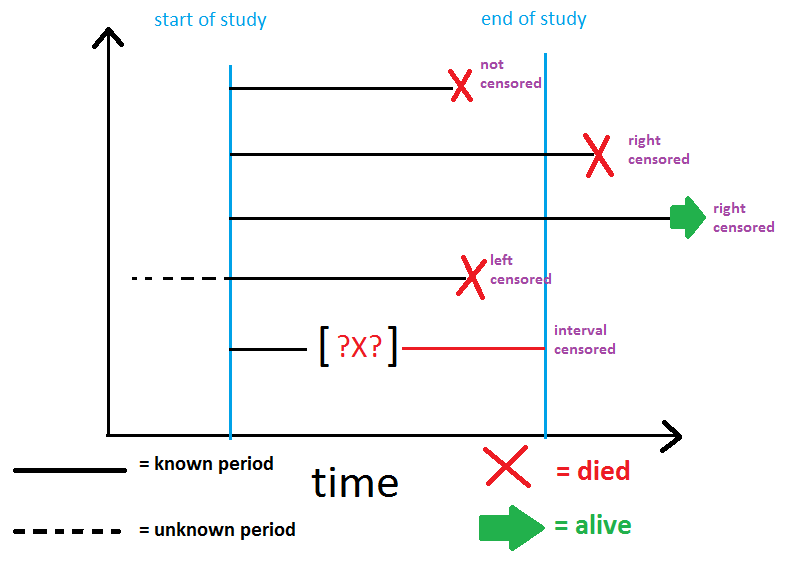
다른 그림은 다음과 같습니다.
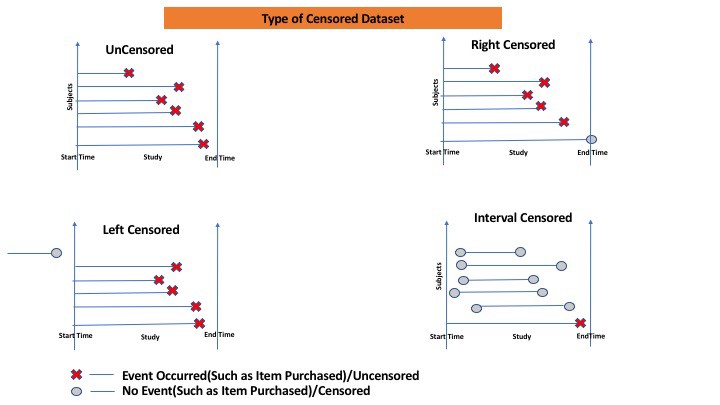
생존 기능
생존 S
즉, 생존 함수는 개인이 시간 t 이후에 생존할 확률입니다.
S
생존 곡선
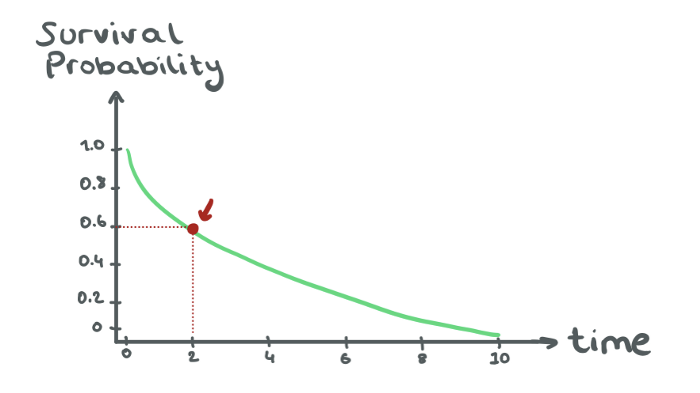
생존 기능 특징
- T ≥ 0 및 0 < t < ∞
- 증가하지 않는다
- 만약에 t = 0이면 S
- 만약에 t=∞이면 S
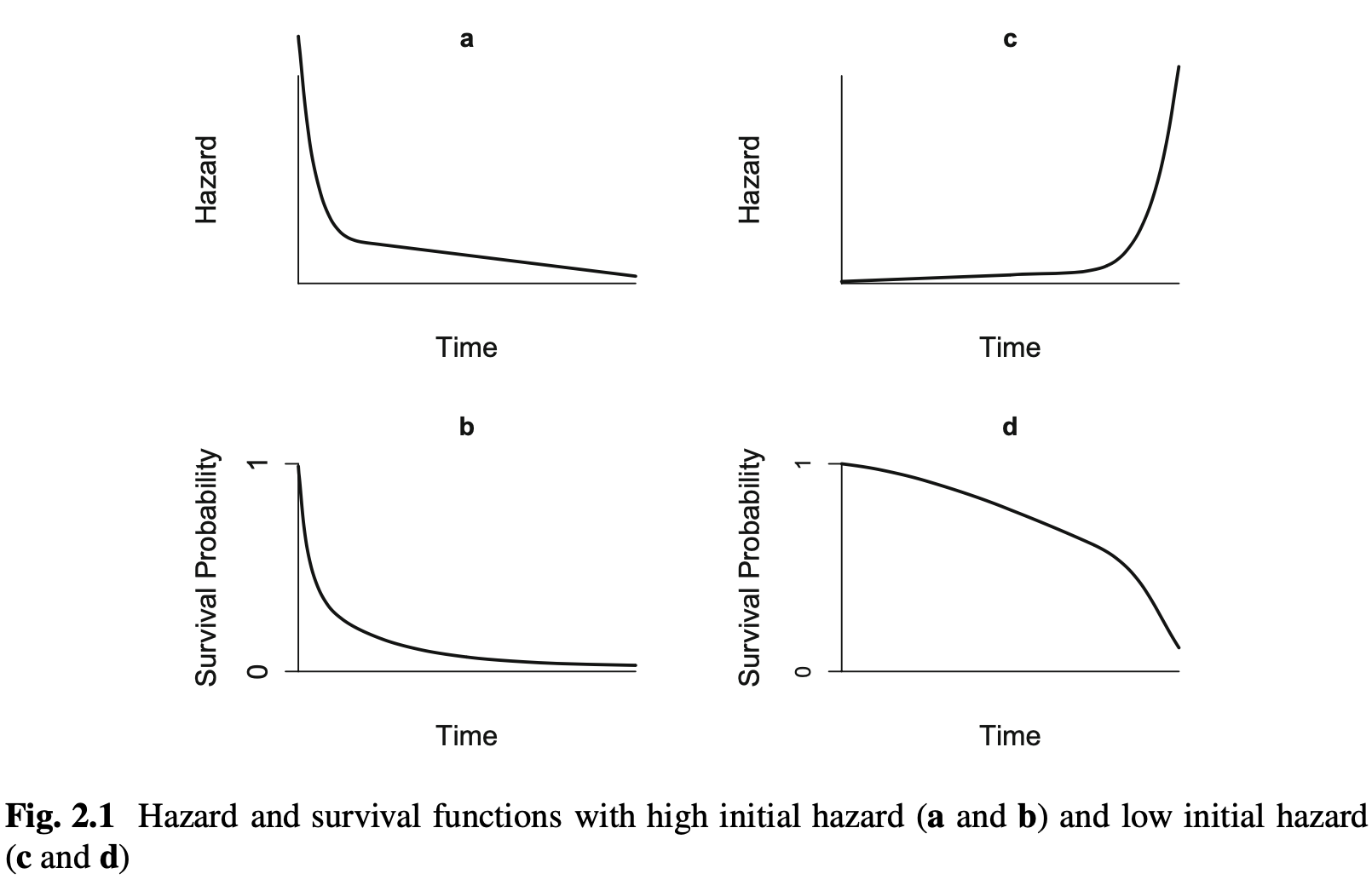
위험 함수
위험 함수는 위험 함수라고도 합니다.
위험 함수 또는 위험률 h
위험 함수와 생존 함수는 다음 공식을 사용하여 서로 도출할 수 있습니다.
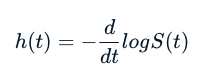

위험 함수가 무엇을 의미하는지 자세히 살펴보겠습니다.
- 위험 함수는 순간적인 의미, 즉 사건이 매우 짧은 시간에 발생할 확률을 의미합니다. 정의에서 알 수 있듯이 매우 짧은 시간에 일어나는 극단적인 의미입니다.
- 위험 함수는 확률로 정의되지만 비율로 이해할 수 있습니다. 위험함수의 정의에서 분모는 확률, 분자는 시간이므로 단위시간당 발생확률로 이해할 수 있다. 또한 위험함수 값이 (0,1) 사이가 아니므로 단위시간당 발생률(
- 위험 함수는 조건부 확률로 정의됩니다. 즉, 모든 개체 이벤트가 아니라 시간입니다. 최대 위험률을 가진 살아있는 유기체입니다.
- 생존 분석에서는 위험 함수가 생존 함수보다 더 중요합니다. 위험 함수의 시간 경과에 따른 추세는 위험이 시간에 따라 변한다는 것을 나타내므로 생존 함수보다 위험의 변화에 대해 더 나은 정보를 제공합니다.

Kaplan-Meier 추정기
기존 생존함수의 경우 특정 분포를 가정할 때만 위험함수를 사용한다.
$f_t$에 대한 분배 가정이 필요하다는 특징이 있습니다.
카플란-마이어(Kaplan-Meier 추정기)비모수 추정기이므로 데이터 분포에 대한 초기 가정이 필요하지 않습니다. 또한 관찰된 생존 시간에 대한 생존 확률을 계산하여 우측 중도절단된 관찰을 처리합니다. 실제로 곱셈 한계 추정기로도 알려진 확률의 곱 규칙을 사용합니다.
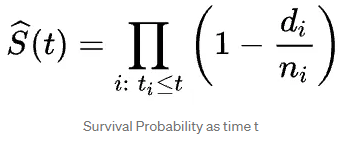
$d_i$ : $t_i$ 시간에 발생한 이벤트 수
$n_i$ : 살아남은 객체의 최대 $t_i$ 수
시간 t_i에서의 생존 확률은 이전 시간 t_{i-1}에서의 생존 확률 곱하기 시간 t_i에서의 생존 확률의 백분율과 같다고 생각할 수 있습니다.

분석하다
KMF를 위한 서바이벌 기능
인용하다
https://towardsdatascience.com/hands-on-survival-analysis-with-python-270fa1e6fb41
https://ilovedata.github.io/teaching/biostat-grad/survival/survivalintro.html
https://www.kaggle.com/datasets/pavansubhasht/ibm-hr-analytics-attrition-dataset